Physics, Rogue Science?

Mathematics

This page re-examines the four main mathematical formulations of special relativity, general relativity and quantum mechanics. I take a position similar to Occam’s Razor, in that I suggest that the most mundane explanation of each equation is likely to be the correct one.

The Lorentz transformation is the core mathematical element in special relativity. It occurs in a variety of situations, including world line diagrams, clocks on trains and platforms, and even the Doppler effect. In this section we see why it is so ubiquitous.
Let’s start with Pythagoras theorem, with c as the hypotenuse:

Then: c² = a² + b²
Rearranging: a² = c² - b²
Divide both sides by c²: a²/c² = c²/c² - b²/c²
Replace b by v, and Square root both sides: a/c = √(1 - v²/ c²)

Where the right hand side of the equation is the Lorentz transformation.

What this shows is that the Lorentz transformation arises in any physical situation where a triangle of velocities can be drawn, and where the hypotenuse represents the speed of light. This is the case in spacetime diagrams of world lines, and also in the earlier diagram of station platforms and passing trains and clocks on both.
What can be calculated is the right hand side of the above equation, representing a proportional change (shown on the left). In this case it is a proportional change in velocity, but the ratio would be the same in any triangle with the same shape, and hence would automatically apply to distances, such as in the Lorentz explanation of the Michelson result.
On an adjunct to this site, Esau James shows that, in his model of matter, such lengths translate directly into frequencies of vibration, and hence atomic timekeeping, the one form of measurement where the Lorentz transformation has been clearly validated.

What we know about this equation is that:

The most used of the different versions of quantum methematics is the Schrödinger equation.
A common version of the Schrödinger equation of quantum mechanics is as follows:

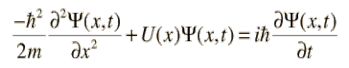
The equation comes in ‘time independent’ and ‘time dependent’ versions. We are interested in the latter, the one that might give us some insight into what is happening at the sub-atomic level moment by moment. The key variable psi (ψ) is not given a physical interpretation in quantum mechanics, but this is actually fairly straightforward, as we shall see shortly.
This is known as a ‘wave equation’ but it clearly is not. Wave equations in physical science have a variable (position) that is differentiated twice with respect to time (giving acceleration) and also differentiated twice with respect to position. This is not the case above where the two derivatives are of different order, so this is not a wave equation.
What we might expect to find in an equation of motion is a term representing acceleration. In the Schrödinger equation this must be the rightmost term, and this suggests that ψ is velocity. When we compare the above equation to the core equation of another major science, this is confirmed:

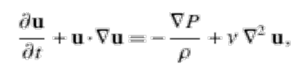
This is a version of the Navier-Stokes equation of hydrodynamics, with u as velocity, and we see straightaway that the derivative structures of the Schrödinger equation are repeated in this equation, with some additional terms.
I therefore suggest that the Schrödinger equation of quantum mechanics is a hydrodynamic equation, that Schrödinger’s ψ is velocity, and that the equation is therefore describing the detailed motion in an underlying substance with the properties of a fluid.
We can go further, and suggest that the use of complex numbers in the Schrödinger equation acts in the same way that it does in other mathematical models, as an efficient description of rotation. If this is the case, then the Schrödinger equation describes a velocity that is orthogonal to both position vector and acceleration, in other words, circular motion.
This is also consistent with the vortex ring model of elementary particles examined in detail by both William Thomson and the unrelated JJ Thomson, and adopted by Esau James.
It is precisely because Mr James’ model fits so neatly with both of the above mathematical reanalyses that he has been invited to present his broader views on this site.
It is worth noting that the version of the time-dependent Schrödinger equation presented above is the ‘one-dimensional’ form, that it only mentions x and not the y and z directions. This is not physically valid in this interpretation, since rotation requires more than one dimension. The above arguments apply therefore to the full time-dependent three-dimensional equation (slightly longer).

Heisenberg produced a mathematical model of what goes on in quantum mechanics a year before Schrödinger. It was a great breakthrough, but doesn’t do as much as Schrödinger’s does, and I do not therefore provide a detailed analysis.
The two mathematical forms look very different. Heisenberg uses matrices. Matrices and the complex numbers used by Schrödinger (above) share some important properties, not least that matrices are also used to describe rotation.

A year after Schrödinger, and two years after Heisenberg, in 1927, Dirac produced yet another version of the mathematics, this one incorporating the Lorentz transformation so as to model fast moving particles.
There are versions of the Dirac equation that look like Heisenberg’s formulation, and versions that look like Schrödinger’s.
I have not provided an analysis of this, as it does not add to our overall understanding.

The two elements of the mathematics of general relativity are the Einstein-Hilbert equation, discussed in the following section, and the Schwarzschild metric.
The key element in the Schwarzschild metric is the following simple formula:
1 – k . m/r
where m is the mass, r the radial distance, and k is a constant calculated from k = G/c².
The following values are well established:
G = universal gravitational constant = 6.672 x 10^-11 N m² kg^-2; c = speed of light = 2.998 x 10⁸ m/s
This gives a value of k = 7.4 x 10^-28 N s² kg^-2
Black holes: Physics believes that gravitational collapse beyond the density of a neutron star can produce a situation where m is so large and r so small that this formula has a value that is zero or negative. I don’t. It is clear that this formula has been checked on a handful of results, all of which have values of k.m/r that are considerably smaller than 1. The formula has never been checked for extreme values of k.m/r, and it is therefore exceedingly poor science to assume that it continues to hold true when the physics and mathematics both become bizarre. The ‘evidence’ for black holes is similarly poor.
Clocks: Just as the Lorentz transformation gives the proportional adjustment to timekeeping due to speed, so the above formula gives the proportional adjustment to timekeeping due to gravity, compared to the rate at which atomic clocks tick when away from gravitational influence.
Clocks in planes, at a height of, say, 10,000 metres, will be less affected than clocks on the ground and therefore tick faster. On a round-the-world flight, they will be at that height for, say, 160,000 seconds, giving a time adjustment of around 175ns, which is approximately what was found by Hafele and Keating and later by Dallas Campbell of the BBC’s programme ‘Bang!’
If you have a calculator, and know the Earth’s mass (say, 6 x 10²⁴kg) and its radius (say, 6,400,000m), you can check the calculation for yourself right now! (Compare the effect for 6,400,000m and for 6,410,000m)
Light speed: Light bends as it passes the Sun, and this has been measured during eclipses, most famously at the Indian Ocean island of Principe in 1919 by Eddington. This can be explained as light travelling more slowly closer to the Sun and more quickly further out, and the wave front consequently slewing around. This interpretation is confirmed by measuring the delay to the signal, which has also been done.
The necessary proportional adjustment to light speed is double that above, namely 2k.m/r. This is handled in the metric by having an equal and opposite adjustment to lengths. Distance divided by time gives an adjustment very close to doubling for the very small adjustments we observe.
It is possible to check both bending and delay calculations using, essentially, first year A-level maths.
Anisotropy: The distance adjustment in the metric is only made to radial distances. There is zero adjustment made to tangential distances. The metric, and by implication relativistic spacetime, is anisotropic, meaning not the same in all directions.
Since light passing the Sun travels both radially (at the start and finish of its travel) and tangentially (at its point of closest approach, slowest speed and maximum rate of bending), physicists (most of those who I have asked) would expect to see both adjustments reflected in the figures for bending and delay. It is a peculiarity of these calculations that they do not. A simplification in Eddingtonⁱⁱ can be used to predict this, but Eddington did not do so.
Unifying theory: One very important effect of this anisotropy is that it make it much harder to unify gravitational relativity with sub-atomic quantum mechanics. It is therefore worth noting that the anisotropy is not supported by any of the observed gravitational effects on timekeeping or bending and delay. It is supported by calculations of advance of perihelion of Mercury, but I have found these unconvincing. The evidence is examined here

You will come across different versions of this, for example:

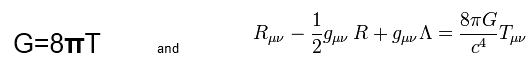
While this doesn’t help communication or clarity, and neither does it help that letters are used differently in different versions (the G and G above, for example), nor that the plus and minus signs in the R version are seen in almost all conceivable combinations, there are much bigger problems in interpreting these equations.
Almost nothing about these equations is readily intelligible. Most letters represent a cluster of further terms, that cluster being sometimes called a matrix and at others, possibly striving for reduced clarity, a tensor. And those further terms are often problematic. The T matrix, for example, operates as a catch-all for measurements of density, pressure, momentum and stress, despite these all having different units. Other terms refer back to Riemannian multi-dimensional geometry. This is a huge set of equations masquerading as a single one, and a set that purports to replace Newtonian gravitational attraction with a mish-mash of just about everything else. It is known to be almost entirely unusable in practical situations.
There are enough volumes of largely mathematical quasi-scientific papers on this equation to fill a library, and it is all over the web like a rash, but I question whether any of it is scientifically worthwhile. These are games played by mathematicians and mathematical physicists, often with the mathematics done badly, and commonly with a disdain for scientific considerations and the objections that have been exposed on this site. There is also an unjustified arrogance towards those who don’t know the rules of the game, not at all warranted by either competence or clarity, features that the general public has a right to expect.
The good news for anyone interested in genuine science in this area is that this equation is validated only by the assertion of mathematical elegance, and even that is questionable. We saw above that all of the properly validated mathematics of general relativity is in two of the four lines of the Schwarzschild metric, and that aspects of the mathematical models that go beyond this are therefore problematic.
The Einstein equation assumes that a single metric for light and matter is appropriate, but, as we have seen here, this is a false and unscientific assumption.
The biggest problem for this equation in its various formulations, therefore, is that it is valueless.

David Hestenes in the US produced a new form of mathematics called geometric algebra. Like much mathematics, it is difficult to understand but then easy to use.
I like GA; it is unexpectedly elegant.
It has been used by my friend Peter Rowlands at Liverpool University to generate the main results in quantum mechanics, and by Chris Doran at Cambridge to do the same in general relativity. Both say, correctly, that these results are much easier to obtain with GA than any other mathematics. Nevertheless, it has not caught on.
GA uses equations that handle mass, momentum and energy together, but keep the three quantities separate in any formula. For this reason, the claim is made for GA that it provides a direct physical insight into modern physics. I have not found this to be the case.

Return to top of page

© Copyright 2013